Computes 2-by-2 orthogonal matrices U, V, and Q, and applies them to matrices A and B such that the rows of the transformed A and B are parallel.
Syntax
call slags2( upper, a1, a2, a3, b1, b2, b3, csu, snu, csv, snv, csq, snq)
call dlags2( upper, a1, a2, a3, b1, b2, b3, csu, snu, csv, snv, csq, snq)
Include Files
The FORTRAN 77 interfaces are specified in the mkl_lapack.fi include file (to be used in Fortran programs) and in the mkl_lapack.h include file (to be used in C programs).
Description
The routine computes 2-by-2 orthogonal matrices U, V and Q, such that if upper = .TRUE., then
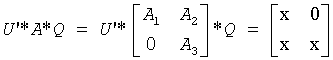
and
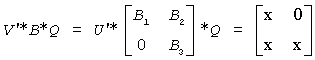
or if upper = .FALSE., then
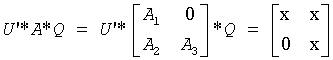
and

The rows of the transformed A and B are parallel, where

Here Z' denotes the transpose of Z.
Input Parameters
- upper
LOGICAL.
If upper = .TRUE., the input matrices A and B are upper triangular; If upper = .FALSE., the input matrices A and B are lower triangular.
- a1, a2, a3
REAL for slags2
DOUBLE PRECISION for dlags2
On entry, a1, a2 and a3 are elements of the input 2-by-2 upper (lower) triangular matrix A.
- b1, b2, b3
REAL for slags2
DOUBLE PRECISION for dlags2
On entry, b1, b2 and b3 are elements of the input 2-by-2 upper (lower) triangular matrix B.