Applies one step of incremental condition estimation.
Syntax
call slaic1( job, j, x, sest, w, gamma, sestpr, s, c )
call dlaic1( job, j, x, sest, w, gamma, sestpr, s, c )
call claic1( job, j, x, sest, w, gamma, sestpr, s, c )
call zlaic1( job, j, x, sest, w, gamma, sestpr, s, c )
Include Files
The FORTRAN 77 interfaces are specified in the mkl_lapack.fi include file (to be used in Fortran programs) and in the mkl_lapack.h include file (to be used in C programs).
Description
The routine ?laic1 applies one step of incremental condition estimation in its simplest version.
Let x, ||x||2 = 1 (where ||a||2 denotes the 2-norm of a), be an approximate singular vector of an j-by-j lower triangular matrix L, such that
||L*x||2 = sest
Then ?laic1 computes sestpr, s, c such that the vector
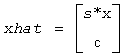
is an approximate singular vector of
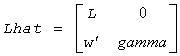
in the sense that
||Lhat*xhat||2 = sestpr.
Depending on job, an estimate for the largest or smallest singular value is computed.
Note that [s c]' and sestpr2 is an eigenpair of the system (for slaic1/claic)

where alpha = x'*w ;
or of the system (for claic1/zlaic)
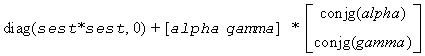
where alpha = conjg(x)'*w.
Input Parameters
- job
INTEGER.
If job =1, an estimate for the largest singular value is computed;
If job =2, an estimate for the smallest singular value is computed;
- j
INTEGER. Length of x and w.
- x, w
REAL for slaic1
DOUBLE PRECISION for dlaic1
COMPLEX for claic1
COMPLEX*16 for zlaic1.
Arrays, dimension (j) each. Contain vectors x and w, respectively.
- sest
REAL for slaic1/claic1;
DOUBLE PRECISION for dlaic1/zlaic1.
Estimated singular value of j-by-j matrix L.
- gamma
REAL for slaic1
DOUBLE PRECISION for dlaic1
COMPLEX for claic1
COMPLEX*16 for zlaic1.
The diagonal element gamma.