Generates an elementary reflector (Householder matrix).
Syntax
call slarfg( n, alpha, x, incx, tau )
call dlarfg( n, alpha, x, incx, tau )
call clarfg( n, alpha, x, incx, tau )
call zlarfg( n, alpha, x, incx, tau )
Include Files
The FORTRAN 77 interfaces are specified in the mkl_lapack.fi include file (to be used in Fortran programs) and in the mkl_lapack.h include file (to be used in C programs).
Description
The routine ?larfg generates a real/complex elementary reflector H of order n, such that
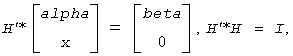
where alpha and beta are scalars (with beta real for all flavors), and x is an (n-1)-element real/complex vector. H is represented in the form
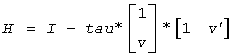
where tau is a real/complex scalar and v is a real/complex (n-1)-element vector. Note that for clarfg/zlarfg, H is not Hermitian.
If the elements of x are all zero (and, for complex flavors, alpha is real), then tau = 0 and H is taken to be the unit matrix.
Otherwise, 1 ≤ tau ≤ 2 (for real flavors), or
1 ≤ Re(tau) ≤ 2 and abs(tau-1) ≤ 1 (for complex flavors).
Input Parameters
- n
INTEGER. The order of the elementary reflector.
- alpha
REAL for slarfg
DOUBLE PRECISION for dlarfg
COMPLEX for clarfg
COMPLEX*16 for zlarfg On entry, the value alpha.
- x
REAL for slarfg
DOUBLE PRECISION for dlarfg
COMPLEX for clarfg
COMPLEX*16 for zlarfg
Array, DIMENSION (1+(n-2)*abs(incx)).
On entry, the vector x.
- incx
INTEGER.
The increment between elements of x. incx > 0.