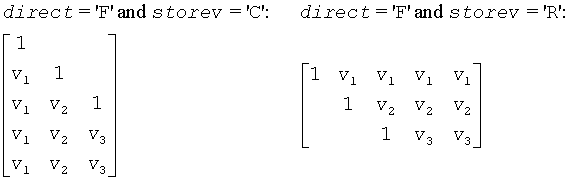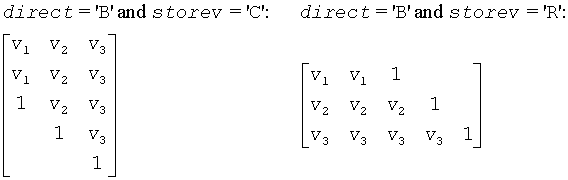Forms the triangular factor T of a block reflector H = I - V*T*V**H.
Syntax
call slarft( direct, storev, n, k, v, ldv, tau, t, ldt )
call dlarft( direct, storev, n, k, v, ldv, tau, t, ldt )
call clarft( direct, storev, n, k, v, ldv, tau, t, ldt )
call zlarft( direct, storev, n, k, v, ldv, tau, t, ldt )
Include Files
The FORTRAN 77 interfaces are specified in the mkl_lapack.fi include file (to be used in Fortran programs) and in the mkl_lapack.h include file (to be used in C programs).
Description
The routine ?larft forms the triangular factor T of a real/complex block reflector H of order n, which is defined as a product of k elementary reflectors.
If direct = 'F', H = H(1)*H(2)* . . .*H(k) and T is upper triangular;
If direct = 'B', H = H(k)*. . .*H(2)*H(1) and T is lower triangular.
If storev = 'C', the vector which defines the elementary reflector H(i) is stored in the i-th column of the array v, and H = I - V*T*V' .
If storev = 'R', the vector which defines the elementary reflector H(i) is stored in the i-th row of the array v, and H = I - V'*T*V.
Input Parameters
- direct
CHARACTER*1.
Specifies the order in which the elementary reflectors are multiplied to form the block reflector:
= 'F': H = H(1)*H(2)*. . . *H(k) (forward)
= 'B': H = H(k)*. . .*H(2)*H(1) (backward)
- storev
CHARACTER*1.
Specifies how the vectors which define the elementary reflectors are stored (see also Application Notes below):
= 'C': column-wise
= 'R': row-wise.
- n
INTEGER. The order of the block reflector H. n ≥ 0.
- k
INTEGER. The order of the triangular factor T (equal to the number of elementary reflectors). k ≥ 1.
- v
REAL for slarft
DOUBLE PRECISION for dlarft
COMPLEX for clarft
COMPLEX*16 for zlarft
Array, DIMENSION
(ldv, k) if storev = 'C' or
(ldv, n) if storev = 'R'.
The matrix V.
- ldv
INTEGER. The leading dimension of the array v.
If storev = 'C', ldv ≥ max(1,n);
if storev = 'R', ldv ≥ k.
- tau
REAL for slarft
DOUBLE PRECISION for dlarft
COMPLEX for clarft
COMPLEX*16 for zlarft
Array, DIMENSION (k). tau(i) must contain the scalar factor of the elementary reflector H(i).
- ldt
INTEGER. The leading dimension of the output array t. ldt ≥ k.
Output Parameters
- t
REAL for slarft
DOUBLE PRECISION for dlarft
COMPLEX for clarft
COMPLEX*16 for zlarft
Array, DIMENSION (ldt,k). The k-by-k triangular factor T of the block reflector. If direct = 'F', T is upper triangular; if direct = 'B', T is lower triangular. The rest of the array is not used.
- v
The matrix V.
Application Notes
The shape of the matrix V and the storage of the vectors which define the H(i) is best illustrated by the following example with n = 5 and k = 3. The elements equal to 1 are not stored; the corresponding array elements are modified but restored on exit. The rest of the array is not used.