Factors an upper trapezoidal matrix by means of orthogonal/unitary transformations.
Syntax
call slatrz( m, n, l, a, lda, tau, work )
call dlatrz( m, n, l, a, lda, tau, work )
call clatrz( m, n, l, a, lda, tau, work )
call zlatrz( m, n, l, a, lda, tau, work )
Include Files
The FORTRAN 77 interfaces are specified in the mkl_lapack.fi include file (to be used in Fortran programs) and in the mkl_lapack.h include file (to be used in C programs).
Description
The routine ?latrz factors the m-by-(m+l) real/complex upper trapezoidal matrix
[A1 A2] = [A(1:m,1:m) A(1: m, n-l+1:n)]
as ( R 0 )* Z, by means of orthogonal/unitary transformations. Z is an (m+l)-by-(m+l) orthogonal/unitary matrix and R and A1 are m-by -m upper triangular matrices.
Input Parameters
- m
INTEGER. The number of rows of the matrix A. m ≥ 0.
- n
INTEGER. The number of columns of the matrix A. n ≥ 0.
- l
INTEGER. The number of columns of the matrix A containing the meaningful part of the Householder vectors.
n-m ≥ l ≥ 0.
- a
REAL for slatrz
DOUBLE PRECISION for dlatrz
COMPLEX for clatrz
COMPLEX*16 for zlatrz.
Array, DIMENSION (lda, n).
On entry, the leading m-by-n upper trapezoidal part of the array a must contain the matrix to be factorized.
- lda
INTEGER. The leading dimension of the array a. lda ≥ max(1,m).
- work
REAL for slatrz
DOUBLE PRECISION for dlatrz
COMPLEX for clatrz
COMPLEX*16 for zlatrz.
Workspace array, DIMENSION (m).
Output Parameters
- a
On exit, the leading m-by-m upper triangular part of a contains the upper triangular matrix R, and elements n-l+1 to n of the first m rows of a, with the array tau, represent the orthogonal/unitary matrix Z as a product of m elementary reflectors.
- tau
REAL for slatrz
DOUBLE PRECISION for dlatrz
COMPLEX for clatrz
COMPLEX*16 for zlatrz.
Array, DIMENSION (m).
The scalar factors of the elementary reflectors.
Application Notes
The factorization is obtained by Householder's method. The k-th transformation matrix, z(k), which is used to introduce zeros into the (m - k + 1)-th row of A, is given in the form
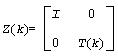
where
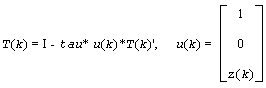
tau is a scalar and z(k) is an l-element vector. tau and z(k) are chosen to annihilate the elements of the k-th row of A2.
The scalar tau is returned in the k-th element of tau and the vector u(k) in the k-th row of A2, such that the elements of z(k) are in a(k, l+1), ..., a(k, n).
The elements of r are returned in the upper triangular part of A1.
Z is given by
Z = Z(1)*Z(2)*...*Z(m).