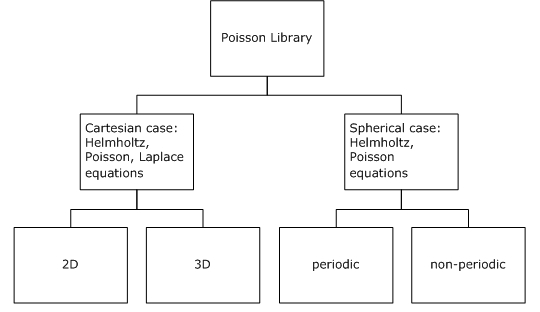
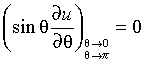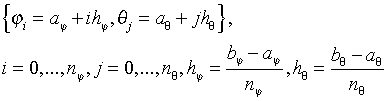PL routines enable approximate solving of certain two-dimensional and three-dimensional problems. Figure "Structure of the Poisson Library" shows the general structure of the Poisson Library.
Sections below provide details of the problems that can be solved using Intel MKL PL.
Two-Dimensional Problems
Notational Conventions
The PL interface description uses the following notation for boundaries of a rectangular domain ax < x < bx, ay < y < by on a Cartesian plane:
bd_ax = {x = ax, ay ≤ y ≤ by}, bd_bx = {x = bx, ay ≤ y ≤ by}
bd_ay = {ax ≤ x ≤ bx, y = ay}, bd_by = {ax ≤ x ≤ bx, y = by}.
The wildcard "+" may stand for any of the symbols ax, bx, ay, by, so that bd_+ denotes any of the above boundaries.
The PL interface description uses the following notation for boundaries of a rectangular domain aφ < φ < bφ, aθ < θ < bθ on a sphere 0 ≤ φ ≤ 2 π, 0 ≤ θ ≤ π:
bd_aφ = {φ = aφ, aθ ≤ θ ≤ bθ}, bd_bφ = {φ = bφ, aθ ≤ θ ≤ bθ}
bd_aθ = {aφ ≤ φ ≤ bφ, θ = aθ}, bd_bθ = {aφ ≤ φ ≤ bφ, θ = bθ}.
The wildcard "~" may stand for any of the symbols aφ, bφ, aθ, bθ, so that bd_~ denotes any of the above boundaries.
Two-dimensional (2D) Helmholtz problem on a Cartesian plane
The 2D Helmholtz problem is to find an approximate solution of the Helmholtz equation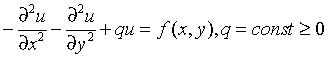
in a rectangle, that is, a rectangular domain ax< x < bx, ay< y < by, with one of the following boundary conditions on each boundary bd_+:
- The Dirichlet boundary condition

- The Neumann boundary condition

where
n= -x on bd_ax, n= x on bd_bx,
n= -y on bd_ay, n= y on bd_by.
Two-dimensional (2D) Poisson problem on a Cartesian plane
The Poisson problem is a special case of the Helmholtz problem, when q=0. The 2D Poisson problem is to find an approximate solution of the Poisson equation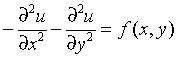
in a rectangle ax< x < bx, ay< y < by with the Dirichlet or Neumann boundary condition on each boundary bd_+. In case of a problem with the Neumann boundary condition on the entire boundary, you can find the solution of the problem only up to a constant. In this case, the Poisson Library will compute the solution that provides the minimal Euclidean norm of a residual.
Two-dimensional (2D) Laplace problem on a Cartesian plane
The Laplace problem is a special case of the Helmholtz problem, when q=0 and f(x, y)=0. The 2D Laplace problem is to find an approximate solution of the Laplace equation
in a rectangle ax< x < bx, ay< y < by with the Dirichlet or Neumann boundary condition on each boundary bd_+.
Helmholtz problem on a sphere
The Helmholtz problem on a sphere is to find an approximate solution of the Helmholtz equation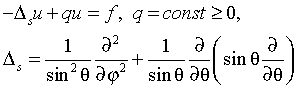
in a spherical rectangle that is, a domain bounded by angles aφ≤ φ ≤ bφ, aθ≤ θ ≤ bθ, with boundary conditions for particular domains listed in Table "Details of Helmholtz Problem on a Sphere".
| Domain on a sphere | Boundary condition | Periodic/non-periodic case |
|---|---|---|
Rectangular, that is, bφ - aφ < 2 π and bθ - aθ < π |
Homogeneous Dirichlet boundary conditions on each boundary bd_~ |
non-periodic |
Where aφ = 0, bφ = 2 π, and bθ - aθ < π |
Homogeneous Dirichlet boundary conditions on the boundaries bd_aθ and bd_bθ |
periodic |
Entire sphere, that is, aφ = 0, bφ = 2 π, aθ = 0, and bθ = π |
periodic |
Poisson problem on a sphere
The Poisson problem is a special case of the Helmholtz problem, when q=0. The Poisson problem on a sphere is to find an approximate solution of the Poisson equation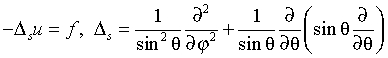
in a spherical rectangle aφ≤ φ ≤ bφ, aθ≤ θ ≤ bθ in cases listed in Table "Details of Helmholtz Problem on a Sphere". The solution to the Poisson problem on the entire sphere can be found up to a constant only. In this case, Poisson Library will compute the solution that provides the minimal Euclidean norm of a residual.
Approximation of 2D problems
To find an approximate solution for any of the 2D problems, a uniform mesh is built in the rectangular domain:
in the spherical case.
Poisson Library uses the standard five-point finite difference approximation on this mesh to compute the approximation to the solution:
In the Cartesian case, the values of the approximate solution will be computed in the mesh points (xi , yj) provided that the user knows the values of the right-hand side f(x, y) in these points and the values of the appropriate boundary functions G(x, y) and/or g(x,y) in the mesh points laying on the boundary of the rectangular domain.
In the spherical case, the values of the approximate solution will be computed in the mesh points (φi , θj) provided that the user knows the values of the right-hand side f(φ, θ) in these points.
 Note
Note
The number of mesh intervals nφ in the φ direction of a spherical mesh must be even in the periodic case. The current implementation of the Poisson Library does not support meshes with the number of intervals that does not meet this condition.
Three-Dimensional Problems
Notational Conventions
The PL interface description uses the following notation for boundaries of a parallelepiped domain ax < x < bx, ay < y <by, az < z <bz:
bd_ax = {x = ax, ay ≤ y ≤ by, az ≤ z ≤ bz}, bd_bx = {x = bx, ay ≤ y ≤ by, az ≤ z ≤ bz}
bd_ay = {ax ≤ x ≤ bx, y = ay, az ≤ z ≤ bz}, bd_by = {ax ≤ x ≤ bx, y = by, az ≤ z ≤ bz}
bd_az = {ax ≤ x ≤ bx, ay ≤ y ≤ by, z = az}, bd_bx = {ax ≤ x ≤ bx, ay ≤ y ≤ by, z = bz}.
The wildcard "+" may stand for any of the symbols ax, bx, ay, by, az, bz, so that bd_+ denotes any of the above boundaries.
Three-dimensional (3D) Helmholtz problem
The 3D Helmholtz problem is to find an approximate solution of the Helmholtz equation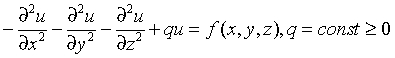
in a parallelepiped, that is, a parallelepiped domain ax< x < bx, ay< y < by, az< z < bz, with one of the following boundary conditions on each boundary bd_+:
- The Dirichlet boundary condition
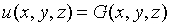
- The Neumann boundary condition

where
n= -x on bd_ax, n= x on bd_bx,
n= -y on bd_ay, n= y on bd_by,
n= -z on bd_az, n= z on bd_bz.
Three-dimensional (3D) Poisson problem
The Poisson problem is a special case of the Helmholtz problem, when q=0. The 3D Poisson problem is to find an approximate solution of the Poisson equation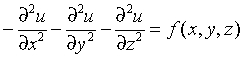
in a parallelepiped ax< x < bx , ay< y < by, az< z < bz with Dirichlet or Neumann boundary condition on each boundary bd_+.
Three-dimensional (3D) Laplace problem
The Laplace problem is a special case of the Helmholtz problem, when q=0 and f(x, y,z)=0. The 3D Laplace problem is to find an approximate solution of the Laplace equation
in a parallelepiped ax< x < bx , ay< y < by, az< z < bz with the Dirichlet or Neumann boundary condition on each boundary bd_+.
Approximation of 3D problems
To find an approximate solution for each of the 3D problems, a uniform mesh is built in the parallelepiped domain![]()

The Poisson Library uses the standard seven-point finite difference approximation on this mesh to compute the approximation to the solution. The values of the approximate solution will be computed in the mesh points (xi , yj , zk), provided that the user knows the values of the right-hand side f(x, y, z) in these points and the values of the appropriate boundary functions G(x, y, z) and/or g(x, y, z) in the mesh points laying on the boundary of the parallelepiped domain.