An example: The fluorine displacement dipole (Born effective charge) in NaF

First we determine the electronic polarization of the undistorted NaF (which, since it is cubic, should be zero).

Calculation 1
We begin by calculating the self-consistent Kohn-Sham potential of the undistorted structure, using a symmetry reduced (4$\times$4$\times$4) Monkhorst-Pack sampling of the Brillouin zone.

KPOINTS file:

4x4x4
 0
Monkhorst
 4 4 4
 0 0 0

POSCAR file:

NaF
 4.5102
 0.0 0.5 0.5
 0.5 0.0 0.5
 0.5 0.5 0.0
1 1
Direct
  0.0000000000000000  0.0000000000000000  0.0000000000000000
  0.5000000000000000  0.5000000000000000  0.5000000000000000

Calculation 2
To calculate the electronic contribution to the polarization, along the ${\bf G}_1$, add the following lines to the INCAR file:

LBERRY = .TRUE.
IGPAR  = 2
NPPSTR = 6
DIPOL = 0.25 0.25 0.25

Setting LBERRY=.TRUE. automatically sets ICHARG=11, since we mean to use the charge density obtained in Calculation 1. The reason for this is that the number of $k$-points, used to evaluate the Berry phase expression can be quite large, large enough for it to be computationally advantageous to use the charge density obatined with the smaller grid used in the previous calculation.

The OUTCAR will now contain something similar to the following lines (grep on ``$<{\rm R}>$"):

Expectation value term: <R>ev
<R>x = (    -0.00001,     0.00000 )
<R>y = (     0.00000,     0.00000 )
<R>z = (     0.00001,     0.00000 )
Berry-Phase term: <R>bp
<R> = (     0.00000,     0.00000,     0.00000 ) electrons Angst
ionic term: <R>ion
<R> = (    20.29590,    20.29590,    20.29590 ) electrons Angst

Calculations 3 and 4
The procedure mentioned under Calculation 2 now has to be repeated with IGPAR=2 and IGPAR=3 (again using the charge density obtained from Calculation 1), to obtain the contributions of the electronic polarization along ${\bf G}_2$ and ${\bf G}_3$, respectively.

Calculations 5-8
To calculate the--change in the--electronic polarization of NaF due to the displacement of the fluorine sublattice, one should repeat Calculations 1-4, using the following POSCAR file:

NaF
 4.5102
 0.0 0.5 0.5
 0.5 0.0 0.5
 0.5 0.5 0.0
1 1
Direct
  0.0000000000000000  0.0000000000000000  0.0000000000000000
  0.5100000000000000  0.5100000000000000  0.4900000000000000

The output of the Berry phase calculation using IGPAR=1 should now be something like this:

Expectation value term: <R>ev
<R>x = (     0.00000,     0.00000 )
<R>y = (     0.00000,     0.00000 )
<R>z = (     0.00116,     0.00000 )
Berry-Phase term: <R>bp
<R> = (     0.00000,     0.17982,     0.17982 ) electrons Angst
ionic term: <R>ion
<R> = (    20.29590,    20.29590,    19.98019 ) electrons Angst

And finally collecting the results
The change in the electronic contribution to the polarization due to the F-sublattice displacement should be calculated as follows:

• Take the average of the $<{\rm R}>_{\rm ev}$ terms obtained in Calculations 2-4. Lets call this $<{\rm R}>_{{\rm ev,undist}}$
• Add the $<{\rm R}>_{\rm bp}$ terms obtained in Calculations 2-4. Lets call this $<{\rm R}>_{{\rm bp,undist}}$
• The electronic polarization of the undistorted structure is then given by:
  
  $$<{\rm R}>_{{\rm el,undist}}=<{\rm R}>_{{\rm ev,undist}}+<{\rm R}>_{{\rm bp,undist}}$$
  
  

• Repeat the above three steps for the results obtained using the distorted structure (Calculations 6-8), to evaluate $<{\rm R}>_{{\rm ev,dist}}$, $<{\rm R}>_{{\rm bp,dist}}$, and $<{\rm R}>_{{\rm el,dist}}$
• The change in the electronic contribution to the polarization due to the F-sublattice displacement, $\Delta<{\rm R}>_{\rm el}$, is then simply found as $<{\rm R}>_{{\rm el,dist}}-<{\rm R}>_{{\rm el,undist}}$

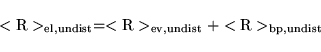
To calculate the total change in polarization, $\Delta<{\rm R}>$, one should take account of the ionic contribution to this change. This can be simply calculated from the $<{\rm R}>_{\rm ion}$ as written in for instance Calculations 2 and 6. $\Delta<{\rm R}>$ is then given by $\Delta<{\rm R}>_{\rm ion}+\Delta<{\rm R}>_{\rm el}$. In this example we find $\Delta<{\rm R}>=0.04393$ electrons/Å. Considering we moved the F-sublattice by 0.045102 Å, this calculation yields a Born effective charge for fluorine in NaF of $Z^{*}=-0.9740$.

N.B.(I) One should take care of the fact that the calculated ``Berry phase" term, $<{\rm R}>_{\rm bp}$ along ${\bf G}_i$, is in principle obtained modulo a certain period, determined by the lattice vector ${\bf R}_{i}$ for which ${\bf R}_{i}\cdot{\bf G}_{i}=2\pi$, the spin multiplicity of the wave functions, the volume of the unit cell, the number of $k$-point in the ``perpendicular" grid, and some aspects of the symmetry of the system. More information on this particular aspect of the Berry phase calculations can be found in Refs. [61], and [63].

N.B.(II) In case of spinpolarized calculations (ISPIN=2) the Berry phase of the wavefunctions is evaluated separately for each spin direction. This means a grep on ``$<{\rm R}>$" will yield two sets of $<{\rm R}>_{\rm ev}$ and $<{\rm R}>_{\rm bp}$ terms, which have to added to oneanother to obtain the total electronic polarization of the system.