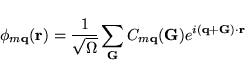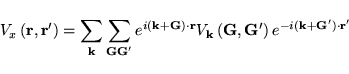


Next: LHFCALC
Up: HF type calculations
Previous: HF type calculations
Contents
The non-local Fock exchange energy, 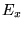 , (in real space) can be written as
, (in real space) can be written as
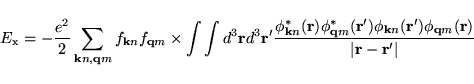 |
(19) |
with
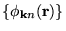 being the set of one-electron
Bloch states of the system, and
being the set of one-electron
Bloch states of the system, and
 the corresponding
set of (possibly fractional) occupational numbers.
The sums over
the corresponding
set of (possibly fractional) occupational numbers.
The sums over 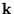 and
and 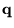 run over all
run over all 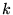 -points chosen to sample the
Brillouin zone (BZ), whereas the sums over
-points chosen to sample the
Brillouin zone (BZ), whereas the sums over 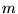 and
and  run over all bands at these
run over all bands at these
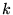 -points.
-points.
The corresponding non-local Fock potential is given by
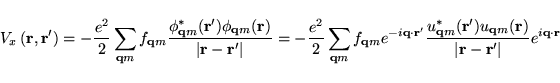 |
(20) |
where
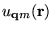 is the cell periodic part of the Bloch state,
is the cell periodic part of the Bloch state,
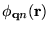 , at
, at 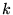 -point,
-point, 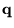 , with band index
, with band index 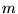 .
.
Using the decomposition of the Bloch states,
 , in plane waves,
, in plane waves,
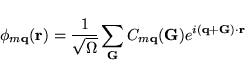 |
(21) |
Equ. (6.14) can be rewritten as
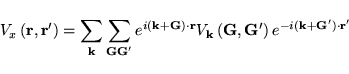 |
(22) |
where
 |
(23) |
is the representation of the Fock potential in reciprocal space.
Note: For a comprehensive description of the implementation of the
Fock-exchange operator within the PAW formalism see Ref. [66]



Next: LHFCALC
Up: HF type calculations
Previous: HF type calculations
Contents
Georg Kresse
2009-04-23
![]() , (in real space) can be written as
, (in real space) can be written as
![]() , in plane waves,
, in plane waves,