

Next: LSELFENERGY: the frequency dependent
Up: Frequency dependent GW calculations
Previous: ENCUTGWSOFT soft cutoff for
Contents
EVENONLYGW = logical
ODDONLYGW = logical
ODDONLYGW allows to avoid the inclusion
of the 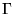 -point in the evaluation of response functions.
The independent particle polarizability
-point in the evaluation of response functions.
The independent particle polarizability
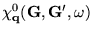 is given by:
is given by:
 |
(42) |
If the 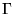 point is included in the summation over
point is included in the summation over 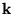 , convergence
is very slow for some materials (e.g. GaAs).
, convergence
is very slow for some materials (e.g. GaAs).
To deal with this problem the flag ODDONLYGW has been included.
In the automatic mode, the 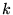 -grid is given by (see Sec. 5.5.3):
-grid is given by (see Sec. 5.5.3):
If the three integers 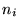 sum to an odd value, the
sum to an odd value, the 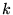 -point is included in the previous summation in the GW routine ( ODDONLYGW=.TRUE.).
Note that other routines (linear optical properties) presently do not recognize this flag.
EVENONLYGW =.TRUE. is only of limited use and restricts the summation to
-point is included in the previous summation in the GW routine ( ODDONLYGW=.TRUE.).
Note that other routines (linear optical properties) presently do not recognize this flag.
EVENONLYGW =.TRUE. is only of limited use and restricts the summation to
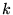 -points with
-points with 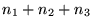 being even (
being even (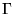 -point and from there on ever second k-point included).
-point and from there on ever second k-point included).
Accelerations are also possible by evaluating the response function
itself at a restricted number of 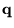 -points.
Note that the GW loop, involves a sum over
-points.
Note that the GW loop, involves a sum over
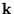 , and a second one over
, and a second one over 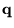 (the index in the response function). To
some extend both can be varied independently. The former one by
using ODDONLYGW, and the latter one
using the HF related flags NKRED, NKREDX, NKREDY, NKREDZ and EVENONLY, ODDONLY.
As explained in Sec. 6.64.8 the index
(the index in the response function). To
some extend both can be varied independently. The former one by
using ODDONLYGW, and the latter one
using the HF related flags NKRED, NKREDX, NKREDY, NKREDZ and EVENONLY, ODDONLY.
As explained in Sec. 6.64.8 the index 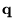 can be restricted to the values
can be restricted to the values
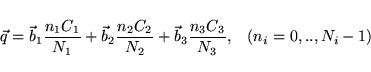 |
(43) |
The integer grid reduction factors are either set separately through
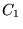 = NKREDX,
= NKREDX, 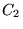 = NKREDY, and
= NKREDY, and 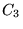 = NKREDZ, or simultaneously
through
= NKREDZ, or simultaneously
through 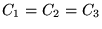 = NKRED.
= NKRED.



Next: LSELFENERGY: the frequency dependent
Up: Frequency dependent GW calculations
Previous: ENCUTGWSOFT soft cutoff for
Contents
Georg Kresse
2009-04-23
![]() -point in the evaluation of response functions.
The independent particle polarizability
-point in the evaluation of response functions.
The independent particle polarizability
![]() is given by:
is given by:
![]() -grid is given by (see Sec. 5.5.3):
-grid is given by (see Sec. 5.5.3):
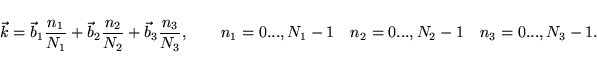
![]() -points.
Note that the GW loop, involves a sum over
-points.
Note that the GW loop, involves a sum over
![]() , and a second one over
, and a second one over ![]() (the index in the response function). To
some extend both can be varied independently. The former one by
using ODDONLYGW, and the latter one
using the HF related flags NKRED, NKREDX, NKREDY, NKREDZ and EVENONLY, ODDONLY.
As explained in Sec. 6.64.8 the index
(the index in the response function). To
some extend both can be varied independently. The former one by
using ODDONLYGW, and the latter one
using the HF related flags NKRED, NKREDX, NKREDY, NKREDZ and EVENONLY, ODDONLY.
As explained in Sec. 6.64.8 the index ![]() can be restricted to the values
can be restricted to the values