NKRED = integer NKREDX= integer NKREDY= integer NKREDZ= integer EVENONLY = logical ODDONLY = logicalUnder certain circumstances it is possible to evaluate the HF kernel (see Equ. 6.13) on a sub grid of
Consider the description of a certain bulk system, using a supercell made up
of ![]() primitive cells, in such a way that,
primitive cells, in such a way that,
![]() , the lattice vectors
of the supercell are given by
, the lattice vectors
of the supercell are given by
![]() (
(![]() ),
where
),
where ![]() are the lattice vectors of the primitive cell.
Let
are the lattice vectors of the primitive cell.
Let
![]() be the distance for which
be the distance for which
![\begin{displaymath}
V_x[\mu]\left({\bf r},{\bf r}'\right)=
-\frac{e^2}{2}\sum_m ...
...\mu\vert{\bf r}-{\bf r}'\vert)}
{\vert {\bf r}-{\bf r}' \vert}
\end{displaymath}](img349.gif) |
(31) |
![\begin{displaymath}
V_x[\mu]\left({\bf r},{\bf r}'\right)=
-\frac{e^2}{2}\sum_{{...
...\mu\vert{\bf r}-{\bf r}'\vert)}
{\vert {\bf r}-{\bf r}' \vert}
\end{displaymath}](img351.gif) |
(32) |
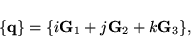 |
(33) |
In light of the above it is clear that the number of ![]() -points needed to represent
the short-ranged Fock potential decreases with decreasing
-points needed to represent
the short-ranged Fock potential decreases with decreasing ![]() (i.e., with increasing
(i.e., with increasing ![]() ).
Furthermore, one should realize that the maximal range of the exchange interactions
is not only limited by the
).
Furthermore, one should realize that the maximal range of the exchange interactions
is not only limited by the
![]() kernel, but depends on the extend of the spatial overlap of the wavefunctions as well
[this can easily be shown for the Fock exchange energy when one adopts a Wannier
representation of the wavefunctions in Eqs. (6.13) or (6.21)];
kernel, but depends on the extend of the spatial overlap of the wavefunctions as well
[this can easily be shown for the Fock exchange energy when one adopts a Wannier
representation of the wavefunctions in Eqs. (6.13) or (6.21)];
![]() , as defined in Equ. (6.24), therefore, provides an upper limit
for the range of the exchange interactions, consistent with maximal spatial
overlap of the wavefunctions.
, as defined in Equ. (6.24), therefore, provides an upper limit
for the range of the exchange interactions, consistent with maximal spatial
overlap of the wavefunctions.
It is thus well conceivable that the situation arises where the short-ranged Fock
potential may be represented on a considerably coarser mesh of points in the BZ than
the other contributions to the Hamiltonian.
To take advantage of this situation one may, for instance, restrict the sum over
![]() in Equ. (6.22) to a subset,
in Equ. (6.22) to a subset, ![]() , of the full
(
, of the full
(
![]() )
) ![]() -point set,
-point set, ![]() , for which the
following holds
, for which the
following holds
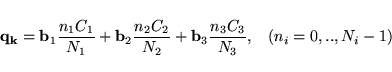 |
(34) |
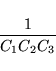 |
(35) |
The integer grid reduction factor are either set separately through
![]() = NKREDX,
= NKREDX, ![]() = NKREDY, and
= NKREDY, and ![]() = NKREDZ, or simultaneously
through
= NKREDZ, or simultaneously
through ![]() = NKRED.
The flag EVENONLY chooses a subset of
= NKRED.
The flag EVENONLY chooses a subset of ![]() points with
points with ![]() ,
and
,
and ![]() even. It reduces the computational work load for HF
type calculations by a factor two, but is only sensible for
high symmetry cases (such as sc, fcc or bcc cells).
even. It reduces the computational work load for HF
type calculations by a factor two, but is only sensible for
high symmetry cases (such as sc, fcc or bcc cells).
Note: From occurrence of the range-separation parameter ![]() in
the equation above, one should not get the impression that the grid reduction can only be
used/useful in conjunction with the HSE03/HSE06 functional
(see Sec. 6.64.7).
It can be applied in the PBE0 and pure HF cases as well, although from the
above it might be clear that the HSE03, in general, will allow for a larger
reduction of the grid than the before-mentioned functionals (see Ref. [73]).
in
the equation above, one should not get the impression that the grid reduction can only be
used/useful in conjunction with the HSE03/HSE06 functional
(see Sec. 6.64.7).
It can be applied in the PBE0 and pure HF cases as well, although from the
above it might be clear that the HSE03, in general, will allow for a larger
reduction of the grid than the before-mentioned functionals (see Ref. [73]).