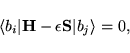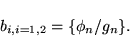


Next: Efficient single band eigenvalue-minimization
Up: Algorithms used in VASP
Previous: Simple Davidson iteration scheme
Contents
Single band, steepest descent scheme
The Davidson iteration scheme optimizes all bands simultaneously. Optimizing a single
band at a time would save the storage necessary for the NBANDS gradients.
In a simple steepest descent scheme the preconditioned residual vector 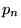 is orthonormalized
to the current set of wavefunctions i.e.
is orthonormalized
to the current set of wavefunctions i.e.
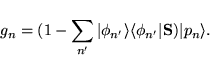 |
(45) |
Then the linear combination of this 'search direction' 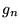 and the current wavefunction
and the current wavefunction 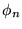 is calculated which minimizes the expectation value of the Hamiltonian.
This requires to solve the
is calculated which minimizes the expectation value of the Hamiltonian.
This requires to solve the 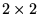 eigenvalue problem
eigenvalue problem
with the basis set
Georg Kresse
2009-04-23
![]() is orthonormalized
to the current set of wavefunctions i.e.
is orthonormalized
to the current set of wavefunctions i.e.