Non-selfconsistent Harris-Foulkes functional

Recently there was an increased interest in the so called Harris-Foulkes (HF) functional. This functional is non selfconsistent: The potential is constructed for some 'input' charge density, then the band-structure term is calculated for this fixed non selfconsistent potential. Double counting corrections are calculated from the input charge density: the functional can be written as

$$\begin{eqnarray*}\vspace*{1mm} E_{\rm HF} [\rho_{\rm in},\rho] & = & \mbox{ban... ...xc}_{\rm in}) \rho_{\rm in}] + E^{\rm xc}[\rho_{\rm in}+\rho_c]. \end{eqnarray*}$$

It is interesting that the functional gives a good description of the binding-energies, equilibrium lattice constants, and bulk-modulus even for covalently bonded systems like Ge. In a test calculation we have found that the pair-correlation function of l-Sb calculated with the HF-function and the full Kohn-Sham functional differs only slightly. Nevertheless, we must point out that the computational gain in comparison to a selfconsistent calculation is in many cases very small (for Sb less than 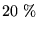$20~\%$). The main reason why to use the HF functional is therefore to access and establish the accuracy of the HF-functional, a topic which is currently widely discussed within the community of solid state physicists. To our knowledge VASP is one of the few pseudopotential codes, which can access the validity of the HF-functional at a very basic level, i.e. without any additional restrictions like local basis-sets etc.

Within VASP the band-structure energy is exactly evaluated using the same plane-wave basis-set and the same accuracy which is used for the selfconsistent calculation. The forces and the stress tensor are correct, insofar as they are an exact derivative of the Harris-Foulkes functional. During a MD or an ionic relaxation the charge density is correctly updated at each ionic step.