


Next: Linear tetrahedron method
Up: Theoretical Background
Previous: Non-selfconsistent Harris-Foulkes functional
Contents
Partial occupancies, different methods
In this section we
discuss partial occupancies. A must for all readers.
First there is the question why to use partial occupancies at
all. The answer is: partial occupancies help to decrease the number
of k-points necessary to calculate an accurate band-structure energy.
This answer might be strange at first sight.
What we want to calculate is, the integral over the filled parts of
the bands
where 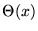 is the Dirac step function. Due to our finite
computer resources this integral has to be evaluated using
a discrete set of k-points[37]:
is the Dirac step function. Due to our finite
computer resources this integral has to be evaluated using
a discrete set of k-points[37]:
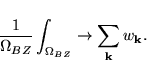 |
(49) |
Keeping the step function we get a sum
which converges exceedingly slow with the number of k-points included.
This slow convergence speed arises only from the fact that
the occupancies jump form 1 to 0 at the Fermi-level.
If a band is completely filled the integral can be calculated
accurately using a low number of k-points (this is the
case for semiconductors and insulators).
For metals the trick is now to replace the step function
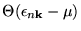 by a (smooth) function
by a (smooth) function
 resulting in a much faster convergence speed
without destroying the accuracy of the sum.
Several methods have been proposed to solve this dazzling problem.
resulting in a much faster convergence speed
without destroying the accuracy of the sum.
Several methods have been proposed to solve this dazzling problem.
Subsections



Next: Linear tetrahedron method
Up: Theoretical Background
Previous: Non-selfconsistent Harris-Foulkes functional
Contents
Georg Kresse
2009-04-23
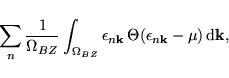
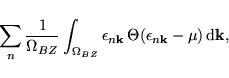
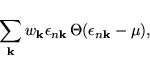
![]() by a (smooth) function
by a (smooth) function
![]() resulting in a much faster convergence speed
without destroying the accuracy of the sum.
Several methods have been proposed to solve this dazzling problem.
resulting in a much faster convergence speed
without destroying the accuracy of the sum.
Several methods have been proposed to solve this dazzling problem.