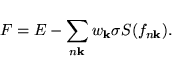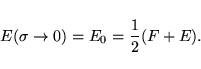


Next: Improved functional form for
Up: Partial occupancies, different methods
Previous: Linear tetrahedron method
Contents
In this case the step function is simply replaced by a smooth
function, for example the Fermi-Dirac function[33]
or a Gauss like function[34]
![\begin{displaymath}\vspace*{1mm}
f(\frac{\epsilon-\mu}{\sigma}) = \frac{1}{2} \...
...erf}
\left [ \frac{\epsilon - \mu}{\sigma} \right ] \right ).
\end{displaymath}](img479.gif) |
(50) |
is one used quite frequently in the context of solid state calculations.
Nevertheless, it turns out that the total energy is no longer
variational (or minimal) in this case. It is necessary to replace the
total energy by some generalized free energy
The calculated forces are now the derivatives of this free energy  (see section 7.5).
In conjunction with Fermi-Dirac statistics
the free energy might be interpreted as the free energy
of the electrons at some finite temperature
(see section 7.5).
In conjunction with Fermi-Dirac statistics
the free energy might be interpreted as the free energy
of the electrons at some finite temperature
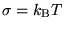 ,
but the physical significance remains unclear in the case
of Gaussian smearing. Despite this problem, it is
possible to obtain an accurate
extrapolation for
,
but the physical significance remains unclear in the case
of Gaussian smearing. Despite this problem, it is
possible to obtain an accurate
extrapolation for 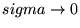 from results at finite
from results at finite  using the formula
using the formula
In this way we get a 'physical' quantity from a
finite temperature calculation, and the Gaussian smearing method
serves as an mathematical tool to obtain faster convergence with respect
to the number of k-points.
For Al this method converges even faster than the
linear tetrahedron method with Bloechel corrections.



Next: Improved functional form for
Up: Partial occupancies, different methods
Previous: Linear tetrahedron method
Contents
Georg Kresse
2009-04-23
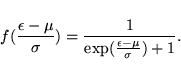
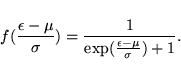
![\begin{displaymath}\vspace*{1mm}
f(\frac{\epsilon-\mu}{\sigma}) = \frac{1}{2} \...
...erf}
\left [ \frac{\epsilon - \mu}{\sigma} \right ] \right ).
\end{displaymath}](img479.gif)