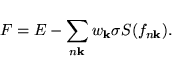


Next: Forces
Up: Partial occupancies, different methods
Previous: Finite temperature approaches
Contents
Table 2:
Typical convenient settings for  for different metals:
Aluminium possesses an extremely simple DOS, Lithium and Tellurium
are also simple nearly free electron metals, therefore
for different metals:
Aluminium possesses an extremely simple DOS, Lithium and Tellurium
are also simple nearly free electron metals, therefore
 might be large. For Copper
might be large. For Copper
 is restricted by the fact that the d-band lies approximately
0.5 eV beneath the Fermi-level. Rhodium and Vanadium posses a fairly
complex structure in the DOS at the Fermi-level,
is restricted by the fact that the d-band lies approximately
0.5 eV beneath the Fermi-level. Rhodium and Vanadium posses a fairly
complex structure in the DOS at the Fermi-level,  must be small.
must be small.
| |
Sigma (eV) |
| Aluminium |
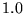 |
| Lithium |
0.4 |
| Tellurium |
0.8 |
| Copper, Palladium |
0.4 |
| Vanadium |
0.2 |
| Rhodium |
0.2 |
| Potassium |
0.3 |
The method described in the last section has two shortcomings:
- The forces calculated by VASP are a derivative of the free electronic
energy F (see section 7.5).
Therefore the forces can not be used to
obtain the equilibrium groundstate, which corresponds to
an energy-minimum of
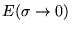 .
Nonetheless the error in the forces is generally small and acceptable.
.
Nonetheless the error in the forces is generally small and acceptable.
- The parameter
 must be chosen with great care. If
must be chosen with great care. If  is too large the energy
is too large the energy
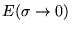 will converge to the
wrong value even for an infinite k-point mesh, if
will converge to the
wrong value even for an infinite k-point mesh, if
 is too small the convergence speed with the number of k-points
will deteriorate. An optimal choice for
is too small the convergence speed with the number of k-points
will deteriorate. An optimal choice for  for several cases is given
in table 2. The only way to get a good
for several cases is given
in table 2. The only way to get a good  is
by performing several calculations with different k-point meshes
and different parameters for
is
by performing several calculations with different k-point meshes
and different parameters for  .
.
These problems can be solved by adopting a slightly different
functional form for
 . This is possible
by expanding the step function in a complete orthonormal set of functions
(method of Methfessel and Paxton [36]).
The Gaussian function is only the first approximation (N=0)
to the step function, further successive approximations (N=1,2,...) are easily obtained.
In similarity to the Gaussian method, the energy has to be replaced
by a generalized free energy functional
. This is possible
by expanding the step function in a complete orthonormal set of functions
(method of Methfessel and Paxton [36]).
The Gaussian function is only the first approximation (N=0)
to the step function, further successive approximations (N=1,2,...) are easily obtained.
In similarity to the Gaussian method, the energy has to be replaced
by a generalized free energy functional
In contrast to the Gaussian method
the entropy term
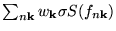 will be very small
for reasonable values of
will be very small
for reasonable values of  (for instance for the values given in table 2).
The
(for instance for the values given in table 2).
The
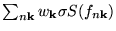 is a simple error estimation for the difference between the
free energy
is a simple error estimation for the difference between the
free energy  and the 'physical' energy
and the 'physical' energy
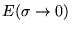 .
.
 can be increased till this error estimation gets too large.
can be increased till this error estimation gets too large.



Next: Forces
Up: Partial occupancies, different methods
Previous: Finite temperature approaches
Contents
Georg Kresse
2009-04-23