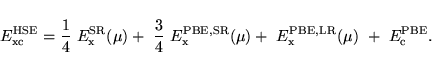 |
(25) |
HFSCREEN = real (truncate the long range Fock potential)In combination with PBE potentials, attributing a value to HFSCREEN will switch from the PBE0 functional (in case LHFCALC=.TRUE.) to the closely related HSE03 or HSE06 functional [67,68,69].
The HSE03 and HSE06 functional replaces the slowly decaying long-ranged part of the
Fock exchange, by the
corresponding density functional counterpart.
The resulting expression for the exchange-correlation energy is given by:
The decomposition of the Coulomb kernel is obtained using the
following construction (![]() HFSCREEN):
HFSCREEN):
Note: It has been shown [67] that the optimum ![]() ,
controlling the range separation is approximately
,
controlling the range separation is approximately ![]() Å
Å![]() . To conform
with the HSE06 functional you need to select ( HFSCREEN=0.2) [67,68,69].
. To conform
with the HSE06 functional you need to select ( HFSCREEN=0.2) [67,68,69].
Using the decomposed Coulomb kernel and Equ. (6.13), one
straightforwardly obtains:
Clearly, the only difference to the reciprocal space representation of the complete (undecomposed) Fock exchange potential, given by Equ. (6.17), is the second factor in the summand in Equ. (6.22), representing the complementary error function in reciprocal space.
The short-ranged PBE exchange energy and potential, and their
long-ranged counterparts, are arrived at using the same decomposition
[Equ. (6.20)], in accordance with Heyd et al. [67]
It is easily seen from Equ. (6.20) that the long-range term becomes
zero for ![]() , and the short-range contribution then equals the full Coulomb
operator, whereas for
, and the short-range contribution then equals the full Coulomb
operator, whereas for
![]() it is the other way around.
Consequently, the two limiting cases of the HSE03/HSE06 functional [see
Equ. (6.19)] are a true PBE0 functional for
it is the other way around.
Consequently, the two limiting cases of the HSE03/HSE06 functional [see
Equ. (6.19)] are a true PBE0 functional for ![]() , and a pure PBE
calculation for
, and a pure PBE
calculation for
![]() .
.
Note: A comprehensive study of the performance of the
HSE03/HSE06 functional compared to the PBE and PBE0 functionals can be found
in Ref. [73].
The B3LYP functional was investigated in Ref. [74].
Further applications of hybrid functionals to selected materials can be found in
the following references:
Ceria (Ref. [75]), lead chalcogenides (Ref. [76]),
CO adsorption on metals (Refs. [77,78]), defects in ZnO
(Ref. [79]), excitonic properties (Ref. [80]),
SrTiO![]() and BaTiO
and BaTiO![]() (Ref. [81]).
(Ref. [81]).
LTHOMAS
If the flag LTHOMAS is set, a similar decomposition of the exchange functional
into a long range and a short range part is used. This time, it is more
convenient to write the decomposition in reciprocal space:
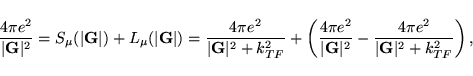 |
(29) |
Thomas-Fermi vector in A = 2.00000Since, VASP counts the semi-core states and